Advanced Vector Space Models : Assignment 5
In this assignment, we will examine some advanced uses of vector representations of words. We are going to look at two different problems:
- Solving word relation problems like analogies using word embeddings.
- Comparing correlation for human judgments of similarity to the vector similarities
- Discovering the different senses of a ‘polysemous’ word by clustering together its paraphrases.
Here are the materials that you should download for this assignment:
part1.txt= a template for answering Part 1part2.py= main code stub for Part 2part3.py= main code stub for Part 3 All Tasksmakecooccurrences.py= script to make cooccurrences (optional use in Part 3 Task 3.2)report.tex= template for the Report (optional use)
Go to the /home1/c/cis530/hw5_2020 on biglab or eniac to download:
- data/
- SimLex-999.txt = Part 2
- dev_input.txt = Part 3 All Tasks
- dev_output.txt = Part 3 All Tasks
- test_input.txt = Part 3 All Tasks
- test_nok_input.txt Part 3 Task 3.4
- vectors/
- GoogleNews-vectors-negative300.magnitude = Part 1 and 2
- glove.6B.100d.magnitude = Part 2
- glove.6B.200d.magnitude = Part 2
- glove.6B.300d.magnitude = Part 2
- glove.6B.50d.magnitude = Part 2
- love.840B.300d.magnitude = Part 2 (not yet uploaded but you can dowload using the following link)
- coocvec-500mostfreq-window-3.filter.magnitude = Part 3 Task 3.2
- reuters.rcv1.tokenized = Part 3 Task 3.2 (optional use)
- GoogleNews-vectors-negative300.filter.magnitude = Part 3 Task 3.3
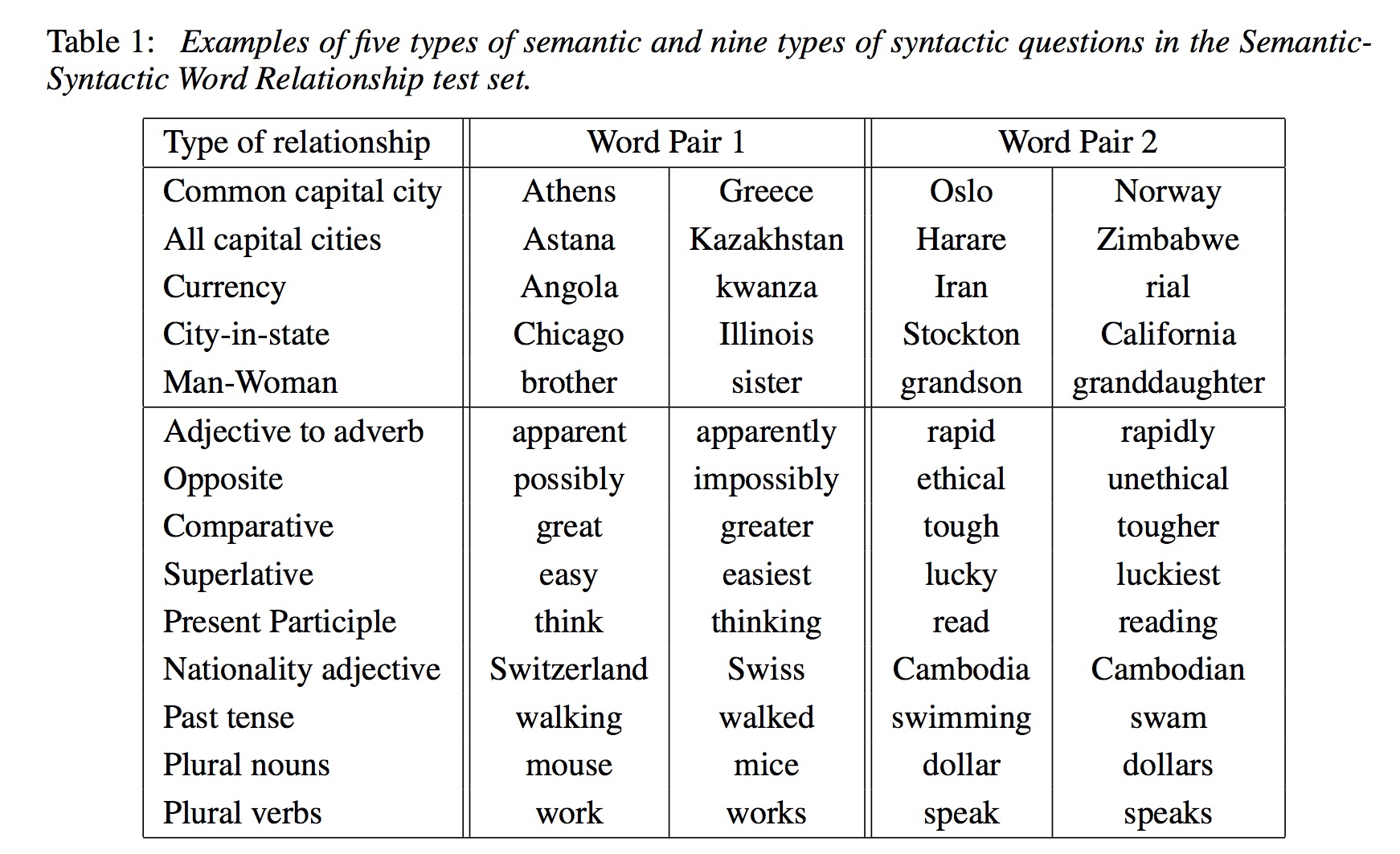
Part 1: Exploring Analogies and Other Word Pair Relationships (10 points)
Background
Word2vec is a very cool word embedding method that was developed by Thomas Mikolov et al. One of the noteworthy things about the method is that it can be used to solve word analogy problems like:
man is to king as woman is to [blank]
The way that it they take the vectors representing king, man and woman and perform some vector arithmetic to produce a vector that is close to the expected answer:
$king−man+woman \approx queen$.
We can find the nearest vector in the vocabulary by looking for $argmax \ cos(x, king-man+woman)$. Omar Levy has an explanation of the method in this Quora post and in the paper.
In addition to solving this sort of analogy problem, the same sort of vector arithmetic was used with word2vec embeddings to find relationships between pairs of words like the following:
Getting Started with Magnitude and Downloading data
In the first part of the assigment, you will play around with the Magnitude library. You will use Magnitude to load a vector model trained using word2vec, and use it to manipulate and analyze the vectors. Please refer here for the installation guidelines.
In order to proceed further, you need to use the Medium Google-word2vec embedding model trained on Google News by using file GoogleNews-vectors-negative300.magnitude on eniac in /home1/c/cis530/hw5_2020/vectors/. Once the file is downloaded use the following Python commands:
>>> from pymagnitude import *
>>> file_path = "GoogleNews-vectors-negative300.magnitude"
>>> vectors = Magnitude(file_path)
Now you can use vectors to perform queries. For instance, you can query the distance of cat and dog in the following way:
>>> vectors.distance("cat", "dog")
0.69145405
Assignment Questions
The questions below are designed to familiarize you with the Magnitude word2vec package and get you thinking about what type of semantic information word embeddings can encode. We recommend reading using the library section to reply to the following set of questions:
- What is the dimensionality of these word embeddings? Provide an integer answer.
- What are the top-5 most similar words to
picnic(not includingpicnicitself)? - According to the word embeddings, which of these words is not like the others?
['tissue', 'papyrus', 'manila', 'newsprint', 'parchment', 'gazette'] - Solve the following analogy:
legis tojumpas X is tothrow.
We have provided a file called part1.txt for you to submit answers to the questions above.
Part 2: SimLex-999 Dataset Revisited (15 points)
Let us revisit SimLex-999 dataset from Extra Credit in Assignment 3. We will use SimLex-999.txt located on eniac in /home1/c/cis530/hw5_2020/data/.
We provided you a script called part2.py that:
- Takes
word1,word2, andSimLexcolumns from theSimLex-999.txtdataset, - Computes the similarity between word1 and word2 using
GoogleNews-vectors-negative300.magnitudefrom Part 1 - Displays correlation for human judgments of similarity to the vector similarities using Kendall’s Tau.
You can see the output of part2.py below:
>>> python part2.py
old,new,1.58,0.2228
smart,intelligent,9.2,0.6495
hard,difficult,8.77,0.6026
happy,cheerful,9.55,0.3838
hard,easy,0.95,0.4710
fast,rapid,8.75,0.4767
happy,glad,9.17,0.7409
short,long,1.23,0.5768
stupid,dumb,9.58,0.8173
weird,strange,8.93,0.8165
wide,narrow,1.03,0.4576
bad,awful,8.42,0.5527
easy,difficult,0.58,0.5891
bad,terrible,7.78,0.6829
hard,simple,1.38,0.2591
smart,dumb,0.55,0.5793
insane,crazy,9.57,0.7339
happy,mad,0.95,0.3920
.
.
.
enter,owe,0.68,0.0004
portray,notify,0.78,0.1455
remind,sell,0.4,0.1480
absorb,possess,5.0,0.2386
join,acquire,2.85,0.2623
send,attend,1.67,0.3135
gather,attend,4.8,0.3329
absorb,withdraw,2.97,0.2169
attend,arrive,6.08,0.3654
>>> correlation, p_value = stats.kendalltau(human_scores, vector_scores)
>>> print(f'Correlation = {correlation}, P Value = {p_value}')
Correlation = 0.30913428432001067, P Value = 2.6592796177777357e-48
In this part of the assignment we would like for you to explore how the Kendall’s Tau correlation changes based on the similarity. You may use the script we provided or create your own script.
Please respond to the following questions in the Report.pdf and include your part2.py script in the final submission:
- What is the least similar 2 pairs of words based on human judgement scores and vector similarity? Do the pairs match?
- What is the most similar 2 pairs of words based on human judgement scores and vector similarity? Do the pairs match?
- Provide correlation scores and p values for the following models on eniac in
/home1/c/cis530/hw5_2020/vectors/:- (Stanford - GloVe Wikipedia 2014 + Gigaword 5 6B Medium 50D)
glove.6B.50d.magnitude - (Stanford - GloVe Wikipedia 2014 + Gigaword 5 6B Medium 100D)
glove.6B.100d.magnitude - (Stanford - GloVe Wikipedia 2014 + Gigaword 5 6B Medium 200D)
glove.6B.200d.magnitude - (Stanford - GloVe Wikipedia 2014 + Gigaword 5 6B Medium 300D)
glove.6B.300d.magnitude - (Stanford - GloVe Common Crawl Medium 300D)
love.840B.300d.magnitude
How do those value compare to each other?
- (Stanford - GloVe Wikipedia 2014 + Gigaword 5 6B Medium 50D)
Extra points will be awarded for creativity and a more thorough qualitative analysis.
Part 3: Creating Word Sense Clusters (75 points)
Background
Many Natural Language Processing (NLP) tasks require knowing the sense of polysemous words, which are words with multiple meanings. For example, the word bug can mean:
- A creepy crawly thing
- An error in your computer code
- A virus or bacteria that makes you sick
- A listening device planted by the FBI
In past research my PhD students and I have looked into automatically deriving the different meaning of polysemous words like bug by clustering their paraphrases. We have developed a resource called the paraphrase database (PPDB) that contains of paraphrases for tens of millions words and phrases. For the target word bug, we have an unordered list of paraphrases including: insect, glitch, beetle, error, microbe, wire, cockroach, malfunction, microphone, mosquito, virus, tracker, pest, informer, snitch, parasite, bacterium, fault, mistake, failure and many others. We used automatic clustering group those into sets like:
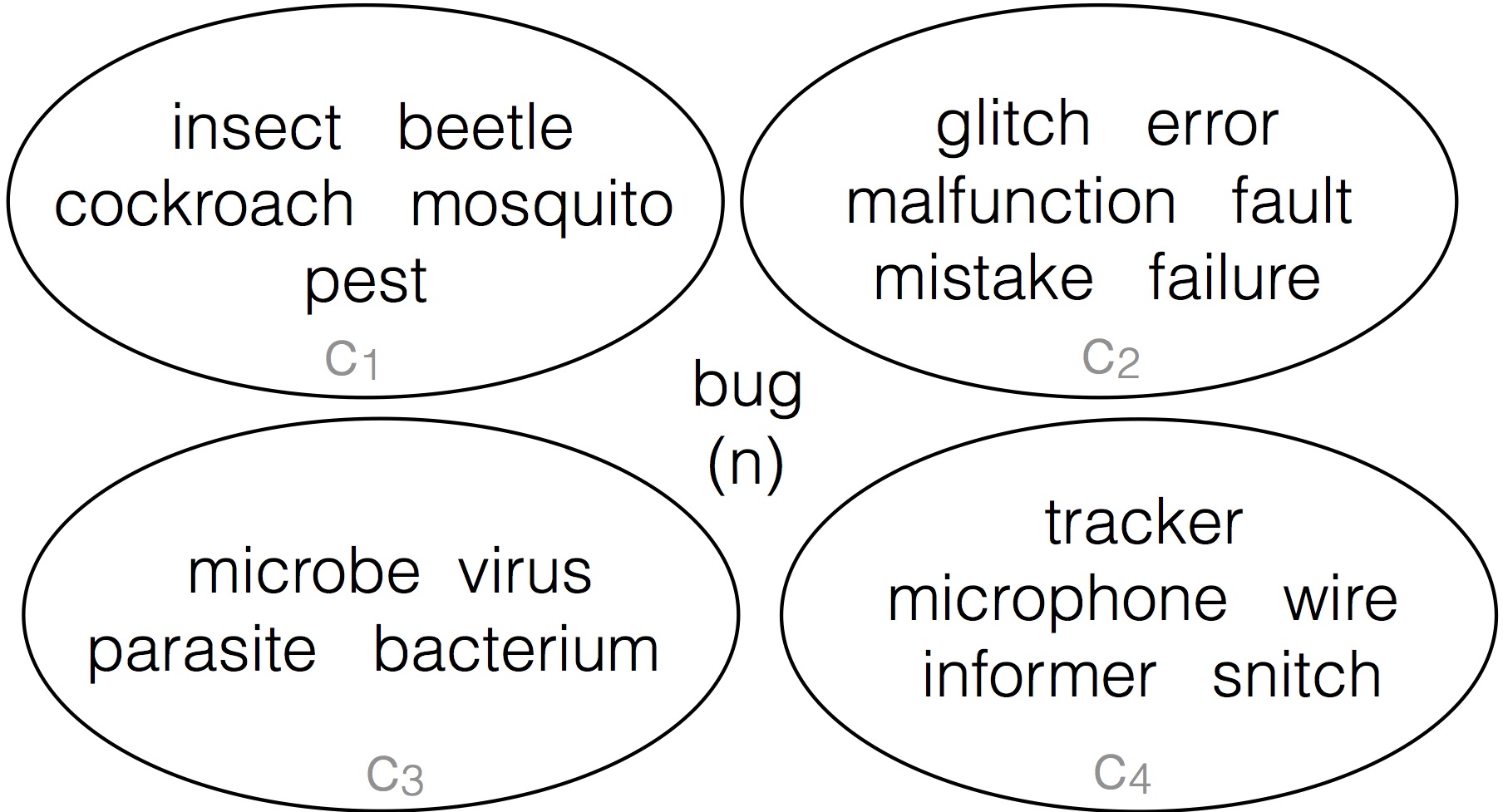
The clusters in the image above approximate the different word senses of bug, where the 4 circles are the 4 senses of bug. The input to this problem is all the paraphrases in a single list, and the task is to separate them correctly. As humans, this is pretty intuitive, but computers are not that smart. You will explore the main idea underlying our word sense clustering method: which measure the similarity between each pair of paraphrases for a target word and then group together the paraphrases that are most similar to each other. This affinity matrix gives an example of one of the methods for measuring similarity that we tried in our paper:
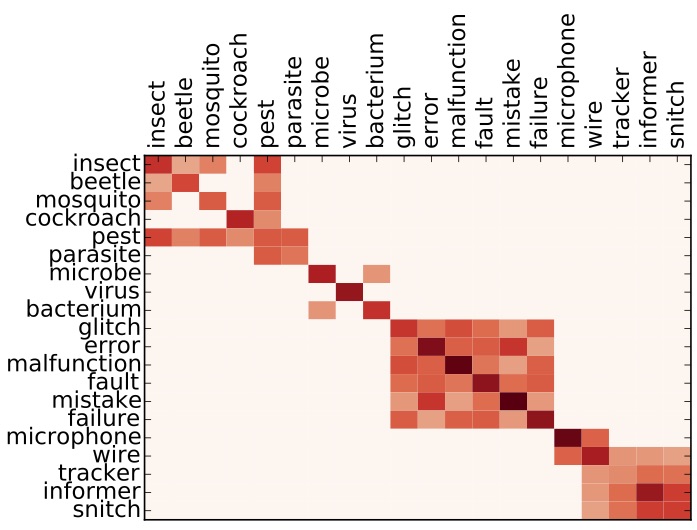
Here the darkness values give an indication of how similar paraphrases are to each other. For instance in this example similarity between insect and pest is greater than the similarity between insect and error. You can read more about this task in these papers.
In this assignment, we will use vector representations in order to measure their similarities of pairs of paraphrases. You will play with different vector space representations of words to create clusters of word senses. We expect that you have read Jurafsky and Martin Chapter 6. Word vectors, also known as word embeddings, can be thought of simply as points in some high-dimensional space. Remember in geometry class when you learned about the Euclidean plane, and 2-dimensional points in that plane? It’s not hard to understand distance between those points – you can even measure it with a ruler. Then you learned about 3-dimensional points, and how to calculate the distance between these. These 3-dimensional points can be thought of as positions in physical space.
Now, do your best to stop thinking about physical space, and generalize this idea in your mind: you can calculate a distance between 2-dimensional and 3-dimensional points, now imagine a point with N dimensions. The dimensions don’t necessarily have meaning in the same way as the X,Y, and Z dimensions in physical space, but we can calculate distances all the same.
This is how we will use word vectors in this assignment: as points in some high-dimensional space, where distances between points are meaningful. The interpretation of distance between word vectors depends entirely on how they were made, but for our purposes, we will consider distance to measure semantic similarity. Word vectors that are close together should have meanings that are similar.
With this framework, we can see how to solve our paraphrase clustering problem.
The Data
The input data to be used for this assignment consists of sets of paraphrases corresponding to one of polysemous target words, e.g.
| Target | Paraphrase set |
|---|---|
| note.v | comment mark tell observe state notice say remark mention |
| hot.a | raging spicy blistering red-hot live |
(Here the .v following the target note indicates the part of speech)
Your objective is to automatically cluster each paraphrase set such that each cluster contains words pertaining to a single sense, or meaning, of the target word. Note that a single word from the paraphrase set might belong to one or more clusters.
Development Data
The development data consists of two files:
- words file (input)
- clusters file (output).
The words file dev_input.txt located on eniac in /home1/c/cis530/hw5_2020/data/ is formatted such that each line contains one target, its paraphrase set, and the number of ground truth clusters k, separated by a :: symbol. You can use k as input to your clustering algorithm.
target.pos :: k :: paraphrase1 paraphrase2 paraphrase3 ...
The clusters file dev_output.txt located on eniac in /home1/c/cis530/hw5_2020/data/ contains the ground truth clusters for each target word’s paraphrase set, split over k lines:
target.pos :: 1 :: paraphrase2 paraphrase6
target.pos :: 2 :: paraphrase3 paraphrase4 paraphrase5
.
.
.
target.pos :: k :: paraphrase1 paraphrase9
Test data
For testing Tasks 3.1 – 3.3, you will receive only words file test_input.txt located on eniac in /home1/c/cis530/hw5_2020/data/ containing the test target words, number of ground truth clusters and their paraphrase sets.
For testing Task 3.4, you will receive only words file test_nok_input.txt located on eniac in /home1/c/cis530/hw5_2020/data/ containing the test target words and their paraphrases sets. Neither order of senses, nor order of words in a cluster matter.
Evaluation
There are many possible ways to evaluate clustering solutions. For this homework we will rely on the paired F-score, which you can read more about in this paper.
The general idea behind paired F-score is to treat clustering prediction like a classification problem; given a target word and its paraphrase set, we call a positive instance any pair of paraphrases that appear together in a ground-truth cluster. Once we predict a clustering solution for the paraphrase set, we similarly generate the set of word pairs such that both words in the pair appear in the same predicted cluster. We can then evaluate our set of predicted pairs against the ground truth pairs using precision, recall, and F-score.
V-Measure is another metric that is used to evaluate clustering solutions, however we will not be using it in this Assignment.
Tasks
Your task is to fill in 4 functions in part2.py: cluster_random, cluster_with_sparse_representation, cluster_with_dense_representation, cluster_with_no_k.
We provided 5 utility functions for you to use:
load_input_file(file_path)that converts the input data (the words file) into 2 dictionaries. The first dictionary is a mapping between a target word and a list of paraphrases. The second dictionary is a mapping between a target word and a number of clusters for a given target word.load_output_file(file_path)that converts the output data (the clusters file) into a dictionary, where a key is a target word and a value is it’s list of list of paraphrases. Each list of paraphrases is a cluster. Remember that Neither order of senses, nor order of words in a cluster matter.get_paired_f_score(gold_clustering, predicted_clustering)that calculates paired F-score given a gold and predicted clustering for a target word.evaluate_clusterings(gold_clusterings, predicted_clusterings)that calculates paired F-score for all target words present in the data and prints the final F-Score weighted by the number of senses that a target word has. 5write_to_output_file(file_path, clusterings)that writes the result of the clustering for each target word into the output file (clusters file)
Full points will be awarded for each of the tasks if your implementation gets above a certain threshold on the test dataset. Please submit to autograder to see thresholds. Note that thresholds are based on the scores from the previous year and might be lowered depending on the average performance.
Task 3.1. Cluster Randomly (10 points)
Write a function cluster_random(word_to_paraphrases_dict, word_to_k_dict) that accepts 2 dictionaries:
- word_to_paraphrases_dict = a mapping between a target word and a list of paraphrases
- word_to_k_dict = a mapping between a target word and a number of clusters for a given target
The function outputs a dictionary, where the key is a target word and a value is a list of list of paraphrases, where a list of paraphrases represents a distinct sense of a target word.
For this task put paraphrases into distinct senses at random. That is, assign to pick a random word for each cluster, as opposed to picking a random cluster for each word. This will ensure that all clusters have at lease one word in them. We recommend using random packages. Please use 123 as a random seed. Your output should look similar to this on the development dataset:
word_to_paraphrases_dict, word_to_k_dict = load_input_file('data/dev_input.txt')
gold_clusterings = load_output_file('data/dev_output.txt')
predicted_clusterings = cluster_random(word_to_paraphrases_dict, word_to_k_dict)
evaluate_clusterings(gold_clusterings, predicted_clusterings)
+----------------+----+----------------+
| Target | k | Paired F-Score |
+----------------+----+----------------+
| paper.n | 7 | 0.2978 |
| play.v | 34 | 0.0896 |
| miss.v | 8 | 0.2376 |
| produce.v | 7 | 0.2335 |
| party.n | 5 | 0.2480 |
| note.v | 3 | 0.6667 |
| bank.n | 9 | 0.1515 |
.
.
.
| eat.v | 6 | 0.2908 |
| climb.v | 6 | 0.2427 |
| degree.n | 7 | 0.2891 |
| interest.n | 5 | 0.2093 |
+----------------+----+----------------+
=> Average Paired F-Score: 0.2318
Run the following command to generate the output file for the predicted clusterings for the test dataset. Please name your output file test_output_random.txt:
word_to_paraphrases_dict, word_to_k_dict = load_input_file('data/test_input.txt')
predicted_clusterings = cluster_random(word_to_paraphrases_dict, word_to_k_dict)
write_to_output_file('test_output_random.txt', predicted_clusterings)
Task 3.2. Cluster with Sparse Representations (20 points)
Write a function cluster_with_sparse_representation(word_to_paraphrases_dict, word_to_k_dict). The input and output remains the same as in Task 1, however the clustering of paraphrases will no longer be random and is based on sparse vector representation.
We will feature-based (not dense) vector space representation. In this type of VSM, each dimension of the vector space corresponds to a specific feature, such as a context word (see, for example, the term-context matrix described in Chapter 6.1.2 of Jurafsky & Martin).
You will calculate cooccurrence vectors on the Reuters RCV1 corpus. It can take a long time to build cooccurrence vectors, so we have pre-built set called coocvec-500mostfreq-window-3.vec.filter.magnitude located on eniac in /home1/c/cis530/hw5_2020/vectors/. To save on space, these include only the words used in the given files.
This representation of words uses a term-context matrix M of size |V| x D, where |V| is the size of the vocabulary and D=500. Each feature corresponds to one of the top 500 most-frequent words in the corpus. The value of matrix entry M[i][j] gives the number of times the context word represented by column j appeared within W=3 words to the left or right of the word represented by row i in the corpus.
If you are interested in building your own cooccurrence vectors, you can use tokenized and cleaned version here called reuters.rcv1.tokenized located on eniac in /home1/c/cis530/hw5_2020/vectors/. The original is here. We used the provided script, makecooccurrences.py, to build these vectors. If you want to use it, be sure to set D and W to what you want. Don’t forget to convert your new vector representation to Magnitude by constructing a Magnitude object.
Use one of the clustering algorithms, for instance K-means clustering in cluster_with_sparse_representation(word_to_paraphrases_dict, word_to_k_dict). Here is an example of the K-means clustering code:
from sklearn.cluster import KMeans
kmeans = KMeans(n_clusters=k).fit(X)
print(kmeans.labels_)As before, run the following command to generate the output file for the predicted clusterings for the test dataset. Please name your output file test_output_sparse.txt:
word_to_paraphrases_dict, word_to_k_dict = load_input_file('data/test_input.txt')
predicted_clusterings = cluster_with_sparse_representation(word_to_paraphrases_dict, word_to_k_dict)
write_to_output_file('test_output_sparse.txt', predicted_clusterings)
Suggestions to improve the performance of your model:
- What if you reduce or increase
Din the baseline implementation? - Does it help to change the window
Wused to extract contexts? - Play around with the feature weighting – instead of raw counts, would it help to use PPMI?
- Try a different clustering algorithm that’s included with the scikit-learn clustering package, or implement your own.
- What if you include additional types of features, like paraphrases in the Paraphrase Database or the part-of-speech of context words?
The only feature types that are off-limits are WordNet features.
Provide a brief description of your method in the Report, making sure to describe the vector space model you chose, the clustering algorithm you used, and the results of any preliminary experiments you might have run on the dev set.
Task 3.3. Cluster with Dense Representations (20 points)
Write a function cluster_with_dense_representation(word_to_paraphrases_dict, word_to_k_dict). The input and output remains the same as in Task 1 and 2, however the clustering of paraphrases is based on dense vector representation.
We would like to see if dense word embeddings are better for clustering the words in our test set. Run the word clustering task again, but this time use a dense word representation.
For this task, we have also included a file called GoogleNews-vectors-negative300.filter.magnitude located on eniac in /home1/c/cis530/hw5_2020/vectors/, which is filtered to contain only the words in the dev/test splits.
As before, use the provided word vectors to represent words and perform one of the clusterings. Here are some suggestions to improve the performance of your model:
- Try downloading a different dense vector space model from the web, like Paragram or fastText.
- Train your own word vectors, either on the provided corpus or something you find online. You can try the skip-gram, CBOW models, or GLOVE. Try experimenting with the dimensionality.
- Retrofitting is a simple way to add additional semantic knowledge to pre-trained vectors. The retrofitting code is available here. Experiment with different lexicons, or even try counter-fitting.
As before, run the following command to generate the output file for the predicted clusterings for the test dataset. Please name your file test_output_dense.txt:
word_to_paraphrases_dict, word_to_k_dict = load_input_file('data/test_input.txt')
predicted_clusterings = cluster_with_dense_representation(word_to_paraphrases_dict, word_to_k_dict)
write_to_output_file('test_output_dense.txt', predicted_clusterings)
Provide a brief description of your method in the Report that includes the vectors you used, and any experimental results you have from running your model on the dev set.
In addition, for Task 3.2 and 3.3, do an analysis of different errors made by each system – i.e. look at instances that the word-context matrix representation gets wrong and dense gets right, and vice versa, and see if there are any interesting patterns. There is no right answer for this.
Task 3.4. Cluster without K (25 points)
So far we made the clustering problem deliberately easier by providing you with k, the number of clusters, as an input. But in most clustering situations the best k is not given.
To take this assignment one step further, see if you can come up with a way to automatically choose k.
Write a function cluster_with_no_k(word_to_paraphrases_dict) that accepts only the first dictionary as an input and produces clusterings for given target words.
We have provided an additional test set test_nok_input.txt located on eniac in /home1/c/cis530/hw5_2020/data/, where the k field has been zeroed out. See if you can come up with a method that clusters words by sense, and chooses the best k on its own.
You can start by assigning k=5 for all target words as a baseline model.
You might want to try and use the development data to analyze how got is your model in determining k.
One of the ways to approach this challenge is to try and select best k for a target word and a list of paraphrases is to use try out a range of k's and judge the performance of the clusterings based on some metric, for instance a silhouette score.
Be sure to describe your method in the Report.
As before, run the following command to generate the output file for the predicted clusterings for the test dataset. Please name your file test_output_nok.txt:
word_to_paraphrases_dict, _ = load_input_file('data/test_nok_input.txt')
predicted_clusterings = cluster_with_no_k(word_to_paraphrases_dict)
write_to_output_file('test_output_nok.txt', predicted_clusterings)
Leaderboards
In order to stir up some friendly competition, we would also like you to submit the clustering from your best model to a leaderboard.
From Task 3.4, copy the output file from your best model to a file called test_nok_output_leaderboard.txt and include it with your submission in ‘HW5: Leaderboard Without K’ following the format of the clusters file.
From Task 3.2 or 3.3, copy the output file from your best model to a file called test_output_leaderboard.txt and include it with your submission in ‘HW5: Leaderboard With K’ following the format of the clusters file.
The first 10 places in either of the two leaderboards get extra points (The exact number of points will be determined).
Report
We are looking for the following sections in your report:
- Part 2 question responses and analysis of correlations
- Task 3.2 description of your model:
- Description of the model
- Clustering algorithm
- Results of any preliminary experiments you might have run on the dev set
- Task 3.3 description of your model:
- Description of the model
- Clustering algorithm
- Results of any preliminary experiments you might have run on the dev set
- Task 3.2 and 3.3 error analysis made by each model:
- i.e. look at instances that the word-context matrix representation gets wrong and dense gets right, and vice versa, and see if there are any interesting patterns.
- Task 3.4 description of your model:
- Description of the model
- Clustering algorithm
- Results of any preliminary experiments you might have run on the dev set
If you wish to write your report in latex, here is a template for you to get started.
Deliverables
Here are the deliverables that you will need to submit:
In HW5: Code:
part1.txt= file with answers to questions from Part 1part2.py= code written / modified for Part 2part3.py= code written for Part 3test_output_random.txt= Task 3.1 output filetest_output_sparse.txt= Task 3.2 output filetest_output_dense.txt= Task 3.3 output filetest_nok_output.txt= Task 3.4 output filemakecooccurrences.py= code written / modified for Part 3
In HW5: Write Up:
Report.pdf
In HW5: Leaderboard Without K
test_nok_output_leaderboard.txt= Task 3.4 output file
In HW5: Leaderboard With K
test_output_leaderboard.txt= Task 3.2 or 3.3 output file
Recommended readings
| Vector Semantics. Dan Jurafsky and James H. Martin. Speech and Language Processing (3rd edition draft) . |
|
Efficient Estimation of Word Representations in Vector Space.
Tomas Mikolov, Kai Chen, Greg Corrado, Jeffrey Dean.
ArXiV 2013.
Abstract
|
|
Linguistic Regularities in Continuous Space Word Representations.
Tomas Mikolov, Wen-tau Yih, Geoffrey Zweig.
NAACL 2013.
Abstract
|
|
Discovering Word Senses from Text.
Patrick Pangel and Dekang Ling.
KDD 2002.
Abstract
|
|
Linguistic Regularities in Sparse and Explicit Word Representations.
Patrick Pangel and Dekang Ling.
CoNLL 2014.
Abstract
|
|
Clustering Paraphrases by Word Sense.
Anne Cocos and Chris Callison-Burch.
NAACL 2016.
Abstract
|
